MA321 Lab 3

Scatterplot

Creating Scatterplots

Scatterplots are statistical graphs using coordinates to display two variables for a set of data pairs. The relationship between variables is called correlation. Scatterplots are used to understand the type and the strength of correlation between two variables.

Example: The following table shows the test average and course overall grades of 20 students.

Test-Average	Course-Overall
80	74
66	65
72	75
76	71
78	61
73	65
74	69
80	79
79	72
80	79
94	95
77	70
65	64
82	73
89	88
92	88
96	96
97	98
88	85
77	75

Draw a scatterplot for the data and use it to answer the following questions.

Does there seems to be a positive linear relationship? Why or why not?
Does the relationship seems strong or weak? Why?

Solution: To draw a scatterplot, you may follow the instructions below.

Step 1: Enter the set of data pairs, say, in the region A1:B21 in a new worksheet.

Step 2: Select data arrays in the range A1:B21.

Step 3: On the Insert tab, click the XY (Scatter) chart command button.

Step 4 (optional): Add a trendline by clicking the Add Chart Element menu’s Trendline command button.

Step 5 (optional): Change bounds for the x-axis by clicking the x-axis and then right clicking to format axis.

Step 6 (optional): Change the title of the picture by clicking the title.

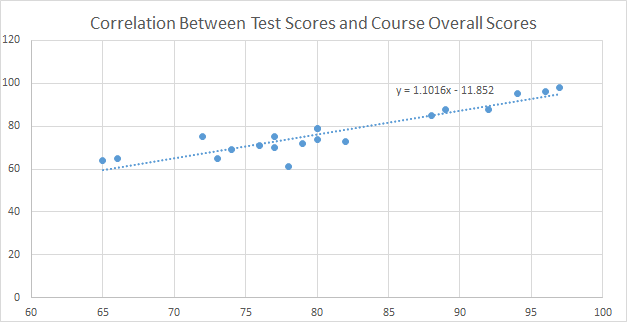
From the scatterplot, we can see that there is a strong positive linear correlation between the test scores and the course overall scores.

Lab Assignment #3

The following data set consists of the midterm and the final exam scores of 20 students.

Midterm	Final
72	72
93	88
81	82
82	82
94	88
80	77
73	78
71	77
81	76
81	76
63	68
73	82
88	89
88	92
96	96
98	97
85	88
75	77
94	95
92	88

Draw a scatterplot for the data and use it to answer the following questions.

Does there seems to be a positive linear relationship? Why or why not?
Does the relationship seems strong or weak? Why?

Test-Average	Course-Overall
80	74
66	65
72	75
76	71
78	61
73	65
74	69
80	79
79	72
80	79
94	95
77	70
65	64
82	73
89	88
92	88
96	96
97	98
88	85
77	75

Midterm	Final
72	72
93	88
81	82
82	82
94	88
80	77
73	78
71	77
81	76
81	76
63	68
73	82
88	89
88	92
96	96
98	97
85	88
75	77
94	95
92	88

Test-Average	Course-Overall
80	74
66	65
72	75
76	71
78	61
73	65
74	69
80	79
79	72
80	79
94	95
77	70
65	64
82	73
89	88
92	88
96	96
97	98
88	85
77	75

Midterm	Final
72	72
93	88
81	82
82	82
94	88
80	77
73	78
71	77
81	76
81	76
63	68
73	82
88	89
88	92
96	96
98	97
85	88
75	77
94	95
92	88

Test-Average	Course-Overall
80	74
66	65
72	75
76	71
78	61
73	65
74	69
80	79
79	72
80	79
94	95
77	70
65	64
82	73
89	88
92	88
96	96
97	98
88	85
77	75

Midterm	Final
72	72
93	88
81	82
82	82
94	88
80	77
73	78
71	77
81	76
81	76
63	68
73	82
88	89
88	92
96	96
98	97
85	88
75	77
94	95
92	88