MA321 Lab 5

Standardization

Given the mean and the standard deviation of a data set, we can use the function STANDARDIZE(value, mean, standard deviation) to convert a data value in it to its standard score, also known as the z-score.

Example: The Stanford-Binet IQ test is scaled so that scores are normally distributed with a mean of 100 and a standard deviation of 15. Find the standard scores for IQ scores of 105.

Solution:

1. Create the following array in a new worksheet in Excel.
   

2. In D2, type in the following formula =STANDARDIZE(C2,A2,B2), then hit enter, the standard scores will show in D2.

Instead, one can use Insert Function to create the formula:

1. Select the cell D2, then click f_x to insert function.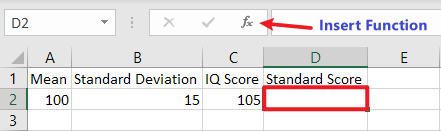
   
2. In the popup windows, search for “standardize”, then select the function and click OK.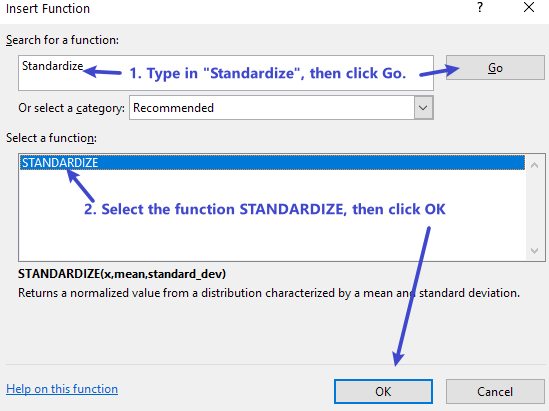
   
3. In the blanks right to X, mean, standard deviation, select the cells C2, A2 and B2, then click OK, you will get the standard score.
   

The standard score is approximately 0.33.

Find the percentile

The percentile is a value below which a given percentage of data fall.

In Excel, to find the percentile, we can use the function NORM.INV(percentage, mean, standard deviation).

Example: The Stanford-Binet IQ test is scaled so that scores are normally distributed with a mean of 100 and a standard deviation of 15. Find the 95th percentile.

Solution:

1. Create the following array in a new worksheet in Excel.
   

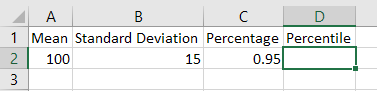
2. In D2, type in the following formula =NORM.INV(C2,A2,B2), then hit enter, the percentile will show in D2.

To create the formula using Insert Function, you may follow the same steps as in the previous example.

The 95 percentile for IQ scores is approximately 125.

Find the percentile rank

The percentile rank of a data value is the percentage of data below the given data value.

In Excel, to find the percentile rank, we can use the function NORM.S.DIST(standard score) if the standard score is know or NORM.DIST(data value, mean, standard deviation, TURE) in general.

Example: The Stanford-Binet IQ test is scaled so that scores are normally distributed with a mean of 100 and a standard deviation of 15. Find the percentile rank of the IQ score 120.

Solution:

Since the standard score is not given, we will use the function NORM.DIST(data value, mean, standard deviation, TURE).

1. Create the following array in a new worksheet in Excel.
   

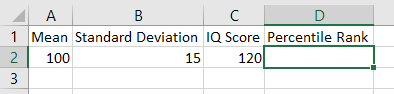
2. In D2, type in the following formula =100*NORM.DIST(C2,A2,B2,TRUE), then hit enter, the percentile rank will show in D2.

To create the formula using Insert Function, you may follow the same steps as in the previous examples.

The IQ score 120 has the percentile rank approximately 91.

Lab Assignment #5

Example: The scores of an uniform final exam is approximate normally distributed with a mean 62 and standard deviation 13.

1. Estimate the 85th percentile.
2. Estimate the percentage of students earned a C or better (that is, 74 or above).

Please show your work in Excel.